Prova 2 — Introdução às Equações Diferenciais Ordinárias

Questão 1#

Enunciado#

Sistemas conservativos unidimensionais: Considere a equação

$$x’’ = F(x)$$

num intervalo da reta. Claramente ela é equivalente ao sistema

$$ \begin{cases} x’ = v \\ v’ = F(x) \end{cases} \tag{1} $$

a) Mostre que a energia total $E = T+U$ é uma integral primeira do sistema, onde $T(v) = \frac{v^2}{2}$ é a energia cinética e $U(x) = - \int_{x_0}^{x} F(\tau)\mathrm{d}\tau$ é a energia potencial.

b) Mostre que todos os pontos de equilíbrio do sistema estão no eixo dos $x.$ Mostre também que todas as órbitas periódicas do sistema interceptam o eixo dos $x$ e são simétricas em relação a ele.

Resolução#

a) vamos calcular qual a derivada $\frac{\mathrm{d}}{\mathrm{d}t} E$ para uma solução do sistema.

$$\frac{\mathrm{d}}{\mathrm{d}t} E$$ $$\frac{\mathrm{d}}{\mathrm{d}t} T + \frac{\mathrm{d}}{\mathrm{d}t} U$$ $$\frac{\mathrm{d}}{\mathrm{d}t} \frac{v^2}{2} - \frac{\mathrm{d}}{\mathrm{d}t} \int_{x_0}^{x} F(\tau)\mathrm{d}\tau$$ $$v v’ - F(x)x’$$ $$x’ F(x) - F(x)x’$$ $$0$$

sendo assim $E$ é constante! De fato uma integral primeira.

b) Um ponto de equilíbrio do sistema precisa satisfazer o sistema

$$ \begin{cases} x’ = v = 0\\ v’ = F(x) = 0 \end{cases} $$

a primeira equação já nos diz que $v = 0$ e que o ponto de equilíbrio precisa estar no eixo dos $x.$

Agora suponha que a solução é periódica, isso é, que existe $\Delta t$ tal que, para todo $t$, vale $x(t + \Delta t) = x(t)$ e $v(t + \Delta t) = v(t)$. Queremos demonstrar que, se $(a, b)$ faz parte de uma órbita, então $(a, -b)$ também faz.

Primeiramente, como $t \mapsto x(t)$ é uma função contínua, ela deve assumir um valor de máximo $x(m)$ no intervalo compacto $[-\Delta t, \Delta t]$. Se o máximo que encontramos está no interior do intervalo, então ele é um ponto crítico. Se o máximo estivesse na borda do compacto, seria um ponto crítico também, porque poderia ser visto como um máximo no interior do intervalo $[0, 2 \Delta t]$. Em todo caso $x’(m) = v(m) = 0$ e essa é a nossa intersecção com o eixo dos $x$.

Além disso, a função $t \mapsto (x(2m - t), -v(2m - t))$ também é uma solução. Como podemos verificar com

$$\frac{\mathrm{d}}{\mathrm{d}t} x(2m - t) = -x’(2m - t) = -v(2m - t)$$

e

$$\frac{\mathrm{d}}{\mathrm{d}t} (-v(2m - t)) = v’(2m - t) = F(x(2m - t))$$

e ela também passa pelo ponto

$$(x(m), v(m)) = (x(m), -v(m)) = (x(m), 0)$$

Daí, pelo teorema de existência e unicidade

$$(x(2m - t), -v(2m - t)) = (x(t), v(t))$$

e as soluções são simétricas em relação ao eixo dos $x$.

Questão 2#

Enunciado#

Seja $\varphi(t, x)$ o fluxo gerado por um campo vetorial $X$ de classe $C^1$ em $\mathbb{R}^1$. Um subconjunto $S \subset \mathbb{R}^n$ não-vazio chama-se minimal (de $X$), se ele é invariante, compacto e não contém subconjuntos próprios com estas propriedades. Prove que em $\mathbb{R}^2$ (i.e., $n = 2$) os únicos subconjuntos minimais de $X$ são os pontos singulares e as órbitas periódicas de $X$. Se $n > 2$, é válido este resultado? Justificar.

Resolução#

Realmente pontos singulares e órbitas periódicas são invariantes. Nenhum subconjunto próprio de nenhum deles serve porque são ambos órbitas. Por definição, dado um ponto da órbita, existe um momento em que a solução passa por lá, então todos os pontos da órbita devem ser incluídos.

Já a volta vem do teorema de Poincaré-Bendixon. Se uma órbita faz parte de um conjunto minimal, o seu conjunto $\omega$-limite também faz. Ele é composto por limites de sequências de pontos do compacto, e sequências no compacto convergem no compacto. O teorema diz que, se não há singularidades, o conjunto $\omega$-limite é uma órbita periódica. Se há singularidades, o $\omega$-limite é uma singularidade ou singularidades conectadas por órbitas homoclínicas ou heteroclínicas. Esta última possibilidade não é um conjunto minimal, visto que o subconjunto das singularidades é invariante. Então as duas primeiras opções são as únicas.

Esse teorema não é necessariamente valido para dimensões maiores. Meu raciocínio é que a equação diferencial

$$\begin{cases} x’ = 1 \\ y’ = \sqrt{2} \end{cases} \tag{3}$$

definida no toro $\mathbb{R}^2/\mathbb{Z}^2$ só tem órbitas não-periódicas e densas em seu domínio. O Teorema de Kronecker nos garante isso. Sendo assim o único conjunto minimal é o próprio domínio, e isso não se encaixa em nenhum dos casos do teorema. Claro que $\mathbb{R}^2/\mathbb{Z}^2$ não é nenhum $\mathbb{R}^n$, mas podemos imergir ele no $\mathbb{R}^4$ com a aplicação

$$(u, v) \mapsto (\sin u, \cos u, \sin v, \cos v)$$

que é uma isometria (mas de $\mathbb{R}^2/2\pi\mathbb{Z}^2$)!. Nessa imersão um exemplo de solução de $(3)$ se torna

$$\varphi(t) = (\sin t, \cos t, \sin \sqrt{2}t, \cos \sqrt{2}t)$$

derivando

$$\varphi’(t) = (\cos t, -\sin t, \sqrt{2}\cos \sqrt{2}t, -\sin \sqrt{2}t)$$

a partir daí podemos relacionar $\varphi$ e $\varphi’$ em uma EDO de primeira ordem.

$$\begin{cases} x_1’ = x_2 \\ x_2’ = -x_1 \\ x_3’ = \sqrt{2}x_4 \\ x_4’ = -\sqrt{2}x_3 \end{cases}$$

que serve como exemplo. Acredito que poderíamos fazer o mesmo com uma imersão do toro em $\mathbb{R}^3$… mas as contas ficariam mais complicadas.

Questão 3#

Enunciado#

Mostre que, para quaisquer valores positivos nos parâmetros $s, r, b$ existe $R > 0$ tal que $V : \mathbb{R}^3 \rightarrow \mathbb{R}$ dada por $V(x, y, z) = rx^2 + sy^2 + s(z - 2r)^2$ é uma função de Lyapunov da equação de Lorenz

$$ \begin{cases} x’ = -sx + sy \\ y’ = rx - y - xz \\ z’ = xy - bz \end{cases} \tag{2} $$

no complementar da bola $B_R(0)$. Conclua que toda trajetória da equação de Lorenz está definida para todo $t \in [0, +\infty)$.

Resolução#

Basta que

$$\langle \nabla V(\mathbf{x}), f(\mathbf{x})\rangle \leq 0$$

para que $V$ seja uma função de Lyapunov. Então primeiro calculemos $\nabla V$

$$\nabla V(x, y, z) = \begin{bmatrix} 2rx \\ 2sy \\ 2s(z-2r) \end{bmatrix}$$

em seguida o produto interno

$$\langle \nabla V(x, y, z), f(x, y, z)\rangle$$

$$2rx(-sx + sy) + 2sy(rx - y - xz) + 2s(z-2r)(xy - bz)$$

$$2s(rx(-x + y) + y(rx - y - xz) + (z-2r)(xy - bz))$$

$$2 s(2 b r z - b z^2 - r x^2 - y^2)$$

$$2 s(b(2 r z - z^2) - r x^2 - y^2)$$

$$2 s(b(r^2 - (z - r)^2) - r x^2 - y^2)$$

essa expressão é menor ou igual a $0$ sempre que $|z-r| \geq r$. Sendo menos específico $|z| \geq 2r$ funciona. Já no caso de $x$ basta que $|x| \geq \sqrt{rb}$ para empurrar a expressão abaixo do $0$. No caso do $y$ basta que $|y| \geq r\sqrt{b}$. Para garantir todas essas inequações ao mesmo tempo, vamos circunscrever uma esfera nesse paralelepípedo.

$$||(x, y, z)|| \geq \sqrt{4r^2 + rb + r^2b}$$

Daí que todas as soluções são limitadas, todas elas estarão contidas dentro dessa esfera depois de certo tempo. Portanto estarão definidas em todo $[0, \infty)$.

Questão 4#

Enunciado#

Seja $f: \mathbb{R}^n \rightarrow \mathbb{R}^n$ de classe $C^1$ tal que $f(0) = 0$. A solução $0 \in \mathbb{R}^n$ diz-se globalmente estável quando for estável e $\lim_{t \rightarrow +\infty} \varphi(t) = 0$ para toda solução $\varphi$ de $x’ = f(x)$. Seja $V: \mathbb{R} \rightarrow \mathbb{R}$ uma função de Liapunov estrita para a EDO em $0$. Suponha que para cada $c > 0$ dado que exista $R > 0$ tal que $|x| > R$ implica $V(x) > c$, para todo $x \in \mathbb{R}^n$. Prove que $0$ é uma solução globalmente estável. Observe que não é necessária a condição $\{ x \in \mathbb{R}^n; V(x) = 0 \} = \{ 0 \}$ e é suficiente supor que este conjunto não contém trajetória inteira e distinta de $x(t) \equiv 0$.

Resolução#

A primeira afirmação que podemos concluir do enunciado é que pra todo $c > 0$ vale que $V^{-1}([0, c])$ é limitado, ele está contido na bola centrada na origem de raio $R$. Além disso é fechado, pré-imagem de uma função contínua em um intervalo fechado. Juntando as duas informações, ele é compacto. Para toda solução $\varphi(t)$ vale $\varphi(t) \in V^{-1}([0, \varphi(t_0)])$.

Como a órbita está dentro do compacto, existe uma sequência de $t_n$’s tais que $\varphi(t_n)$ converge para um ponto que chamaremos $x_1$. Pelo fato de $V$ ser Lyapunov estrita, vale para todo $t$ que

$$V(\varphi(t)) > V(x_1) \tag{🙂}$$

Até aí tudo bem, mas quem é $x_1$? Se $x_1$ for uma singularidade, então precisa ser $0$ para que a solução constante igual a $x_1$ não viole a hipótese de $V$ ser Lyapunov estrita e o teorema está demonstrado. Se $x_1$ não é uma singularidade, então ele tem uma vizinhança tubular, ilustrada abaixo.

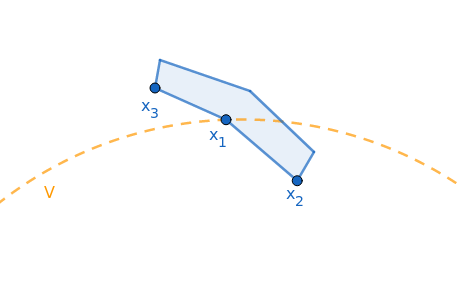
Certamente para $x_2$, o ponto de saída da solução que passa por $x_1$, vale $V(x_2) < V(x_1)$. Pela continuidade do fluxo, existe uma vizinhança na seção transversal de $x_1$ tal que todas as soluções que passem por ela acabem do lado de dentro da curva de nível de $V(x_1)$. Em particular os $\varphi(t_n)$ teriam que passar por essa vizinhança, o que contradiz $(🙂)$.

Em conclusão não há alternativa para as órbitas, elas devem convergir para a origem.